数据结构笔记

01 September 2014

数据结构笔记

二叉树度为2的点有$n_2$个，叶子节点有$n_0$个。证明$n_0==n_2+1$。

证明：总结点个数$n=n_0+n_1+n2$，边的数目为$B=n-1$。度为2的结点贡献出2条边，度为1的结点贡献出1条边。又有$B=n_2+n_1$。结合上述式子，化简得证。

最小生成树算法

普利姆算法

 新增一个辅助数组CloseEdge，维护两个集合U和V-U。U中是已经确定的顶点集合，V-U是未确定的顶点集合。每次从V-U中找一个到U代价最小的点的加入U。时间复杂度是O(顶点数^2)，与边无关，适合稠密图。
 /*
 class CloseEdge
 {
     int adj;
     int lowcost;
 }
 */
 //
 void MiniSpanTree_PRIM(int G[][])
 {
     CloseEdge CloseEdge[]=new CloseEdge();
     for(int i=0;i<G.length;i++)
     {
         CloseEdge[i] = new CloseEdge(0,G[0][i]);
     }
     for(int i=1;i<G.length;i++)
     {
         int k=0,MIN=0x7fffffff;
         for(int j=0;j<G.length;j++)
         {
             if(closeEdge[j].lowcost!=0&&closeEdge[i].lowcost<MIN)
             {
                 k=j;MIN=closeEdge[i].lowcost;
             }
         }
         System.out.printf("边："+closeEdge[k].adj+"到"+k+"加入生成树");
         closeEdge[k].lowcost=0;
         for(int j=0;j<G.length;j++)
         {
             if(G[k][j]<closeEdge[j].lowcost)
             {
                 closeEdge[j].adj=k;
                 closeEdge[j].lowcost=(G[k][j];
             }
         }
     }
 }

克鲁斯卡尔算法

 时间复杂度为O(eloge)，适合求边稀疏的网的最小生成树。
 算法过程：U为空，每次选择代价最小的边，如果这条边能新增节点到U，则要，否则，舍去，选下一代价最小边。

排序树

性能逼近二分查找，优点是插入和删除不需要移动大段内存。但可能改变结构。如下图：

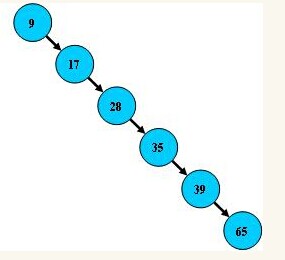
这样查找就是线性的了。所以一般都是维护一个平衡排序树，使左右节点结构尽量平衡。
B-树（即为B树）

B-树一种多路搜索树(并不是二叉的)。M阶B-树的性质：
- 根结点的儿子数为[2, M]；
- 除根结点以外的非叶子结点的儿子数为[M/2, M]；
- 非叶子结点的关键字个数=指向儿子的指针个数-1；（夹着的）
- 叶子节点在同一层，不带关键字信息，可以看做外部节点或查询失败的节点。
- 非叶子节点包括关键字信息，有可能搜索到非叶子节点就终止。
- 搜索性能等价于在关键字内做一个二分查找；
- 关键字分布在整个树中。
- 由于限制了除根节点外的非叶子节点至少包含M/2个儿子，确保了结点的利用率；
B+树

与B-树的差异在于：
- 所有的叶子节点包含了全部关键字的信息，以及指向这些关键字记录的指针，且叶子节点本身依关键字的大小自小而大顺序链接。
- 所有的非叶子节点可以看成索引部分，节点中仅含有其子树的最大（或最小）关键字。
- 更适合文件索引系统；
B*树 在B+树基础上，为非叶子结点也增加链表指针，增加节点的利用率。
为什么使用这些索引树

二叉查找树的结构的查找时间复杂度O($log_2N$)，与树的深度相关，那么降低树的深度自然会提高查找效率。问题背景：树的深度过大而造成磁盘I/O读写过于频繁，进而导致查询效率低下。(所以每个节点存多块数据，这些数据连续，可能都在同一块盘面上，读取时间较短？)

各种操作使B树保持较低的高度。

B树与红黑树最大的不同在于，B树的结点可以有许多子女，从几个到几千个。那为什么又说B树与红黑树很相似呢?因为与红黑树一样，一棵含n个结点的B树的高度也为O（lgn），但可能比一棵红黑树的高度小许多。这里没有考虑磁盘或数据读写时间的比较。因为B数一个节点可能存多个关键字，B树的读写次数是要少很多的。

为什么说B+树比B树更适合做操作系统中的文件索引和数据库索引
- B+树内部没有指向关键字具体信息的指针(就只有指向Key的指针，就是存的东西更少，或者存的空间一样，能存更多关键字)
- 所有查询必须走到叶子节点结束，查询路径长度都相同，更稳定。
- 更方便遍历树，走一遍叶子节点。
- 数据库有许多基于范围的查询频繁，B树不支持这样的操作。因为B+树叶子层是一个有序的，方便范围查询。
- B树的一个优点就是成功查询时可能搜索的高度会比B+树小。
Hash函数的构造方法
- 直接定址法
- 数字分析法
- 平方取中法
- 折叠法
- 取模法（常用，H(key)=key mod p，p一般为质数或无小于20因子的合数）
处理Hash表冲突
- 开放地址法。开放地址就指这个地址没放元素。
  - 线性探测再散列。能保证表未满，就能找到地方放。
    - 优点：思路简单清晰
    - 缺点：
      - 删除工作非常困难。假如要从哈希表 HT 中删除一个记录，按理应将这个记录所在位置置为空，但我们不能这样做，而只能标上已被删除的标记，否则，将会影响以后的查找。
      - 一旦出现堆聚，就将引起进一步的堆聚。
  - 二次探测再散列。表长为4j+3素数才能保证一定有地方放。
  - 随机探测再散列。伪随机数列。
- 再哈希法
- 拉链法(可以头插、尾插以保持在同一链表中关键字有序)
  - 优点：
    - 拉链法处理冲突简单，且无堆积现象，即非同义词决不会发生冲突，因此平均查找长度较短；
    - 空间动态增长
    - 开放定址法为减少冲突，要求装填因子α较小，故当结点规模较大时会浪费很多空间。而拉链法中可取α≥1，且结点较大时，拉链法中增加的指针域可忽略不计，因此节省空间；
    - 易于删除。
  - 缺点：
    - 指针需要额外的空间，故当结点规模较小时，开放定址法较为节省空间。
- 溢出表法
堆排序

大根堆，根节点值最大。找到频率最大的10个整数，肯定使用小根堆，如果比小根堆的根节点大，这个根节点肯定要出去。

如小根堆，取出最小的一个元素后，将堆中最后一个元素置为根节点，然后从根节点自上而下调整： 5 2 3 因为2<3，所以2肯定是新的根节点。2、5调换。依次向下调换直至堆又变成平衡。
稳定的排序：冒泡、插入、归并、基数不稳定的排序：选择、快排、希尔、堆排序

LeetCode 47

数据结构笔记 数据结构知识点笔记

数据结构笔记

数据结构笔记数据结构知识点笔记